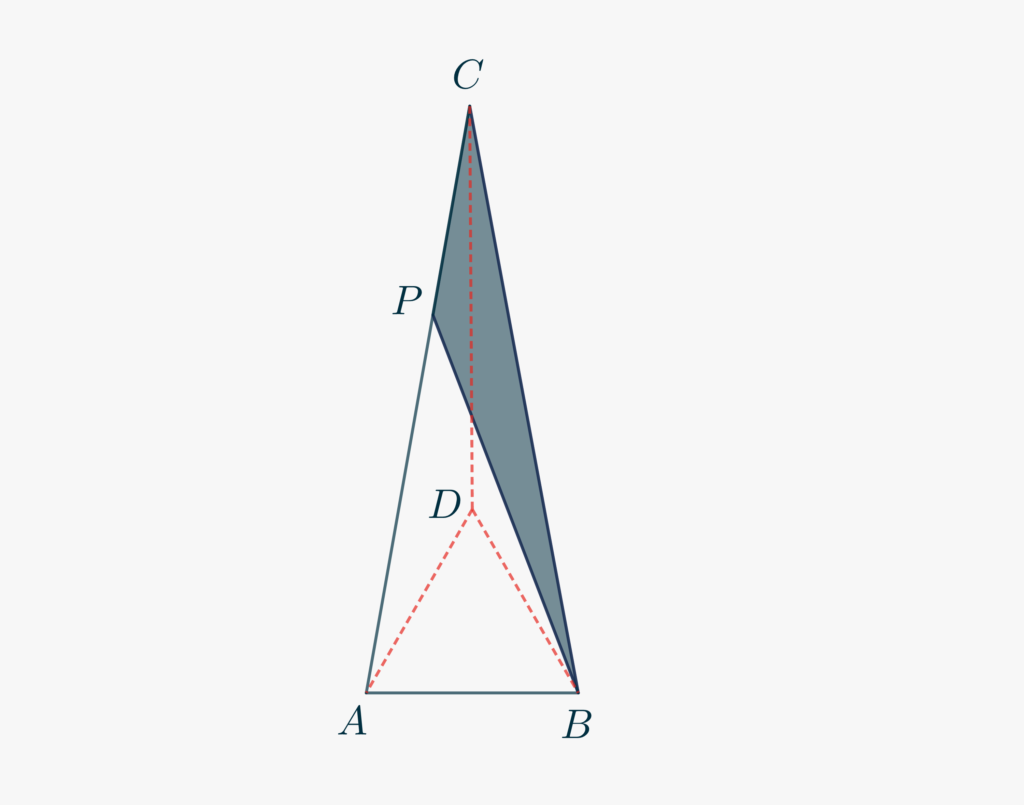
We present another excersise of Euclidean geometry. It is a “classical” problem on the “\(80-80-20\)” isosceles triangle.
Given the isosceles triangle \(\triangle ABC\) with \(\angle ABC = \angle CAB = 80°\), fix a point \(P\) on the side \(AC\) such that \(CP\cong AB\). What is the measure of the angle \(\angle CPB\)?
In order to take advantage of the congruence between \(AB\) and \(CP\) we need to draw some other triangles. For example, we can construct two replicas of \(\triangle ABC\) adjacent to each other, as in the Figure below, where \(\triangle ABC\cong \triangle BCD \cong \triangle CDE\).
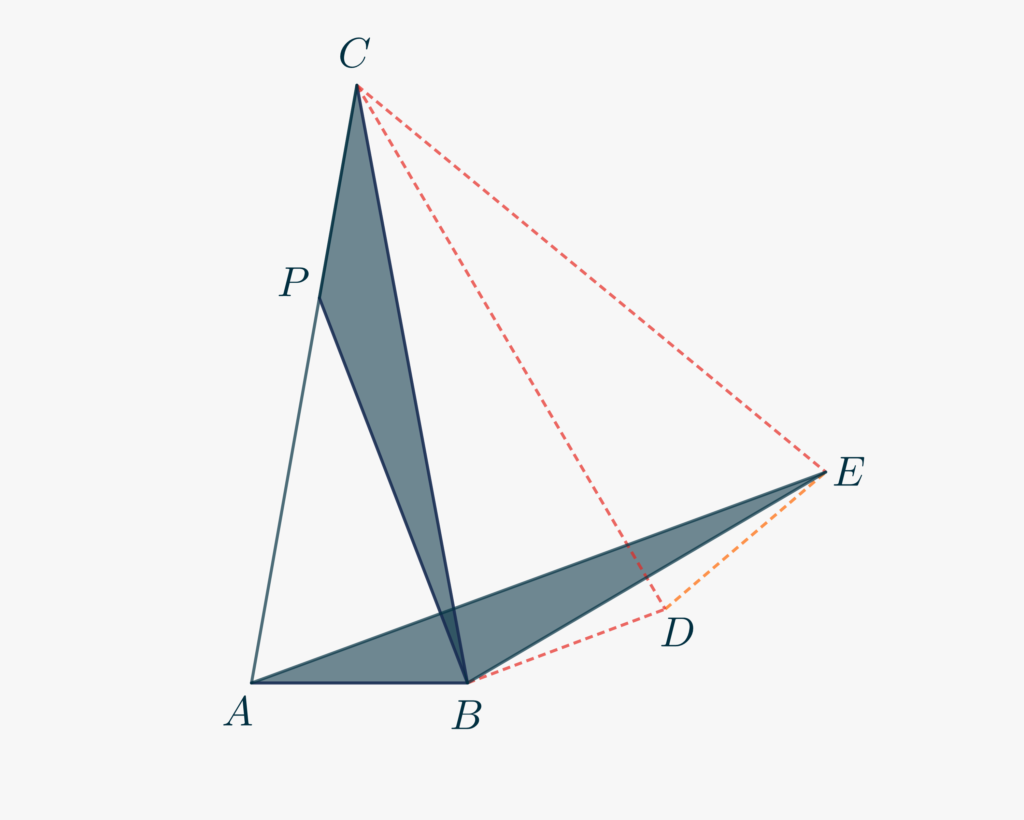
- Triangle \(\triangle ACE\) is isosceles by construction. What can you say about the angle \(\angle ACE\), though?
- Draw then your conclusions on triangle \(\triangle ACE\).
- Determine, by subtraction, the measure of \(\angle EAB\).
- The information you have is enough to state that \(\triangle CPB\) and \(\triangle ABE\) are congruent. Thanks to what congruence criterion?
- Your aim is now to calculate the measure of \(\angle CPB\cong\angle ABE\).
- Concentrate on \(\triangle BDE\). What kind of triangle is that? Why? Use this observation to compute the measure of \(\angle DBE\).
- By correclty using the measure of known angles, determine that of \(\angle ABE\), and, from that, your answer. You should find \(\angle CPB = 150°\).
As an exercise, try to demonstrate the same assertion again, using, this time, the construction below, where \(\triangle ADB\) is equilateral.