Teorema. Sia f una funzione reale, derivabile fino all’ordine n in c∈R, per un qualche intero positivo n. Si supponga che f(n)(c)≠0, e che tutte le derivate di ordine inferiore (se presenti) siano nulle in c. Allora c è un punto estremante se e solo se n è pari.
Nel seguito useremo la notazione f(k)(x), con k>0 per indicare la derivata di ordine k di f in x; per k=0, f(0)(x)=f(x). Assumeremo inoltre, senza perdita di generalità, che c=0, f(0)=0, e f(n)(0)>0.
Avendo informazioni sulla derivata di ordine n in c ma non in un intorno di c, non possiamo utilizzare lo sviluppo di Taylor. Questo è il motivo per cui ho deciso di proporre questo teorema e la sua dimostrazione. Se tuttavia utilizziamo la classica definizione di derivata, come fornita ad esempio in “Principles of Mathematical Analysis” di W. Rudin (def. 5.1, pagina 103), per k=1,2,…, l’esistenza di f(k)(c) implica l’esistenza di f(k−1)(x) in tutto un intervallo che contiene c. Il che ci permetterà di fare uso del Teorema di Lagrange.
Per prima cosa osserviamo che limda cui deduciamo l’esistenza di un intorno \mathcal N of 0 tale per cui \frac{f^{(n-1)}(x)}{x} > 0,\tag{1}\label{eq3769:1}per ogni x \in \mathcal N\setminus \{0\}. Se n=1 la dimostrazione è conclusa, dal momento che dalla \eqref{eq3769:1} f^{(0)}(x)=f(x) segue che la f non ha massimo o minimo locale in 0.
Se n>1, dalla \eqref{eq3769:1} possiamo concludere che f^{(n-2)}(x)>0\tag{2}\label{eq3769:2} per ogni x\in \mathcal N\setminus \{0\}. Possiamo dimostrare ciò per assurdo. Supponiamo infatti esista \overline x \in \mathcal N\setminus \{0\} tale per cui f^{(n-2)}(\overline x)\leq 0. Allora, per il Teorema di Lagrange dovrebbe esistere \xi tale per cui f^{(n-1)}(\xi) = \frac{f^{(n-2)}(\overline x)}{\overline x}. Se \overline x >0, allora 0< \xi <\overline x e f^{(n-1)}(\xi) \leq 0. Se, invece, \overline x < 0, allora \overline x < \xi < 0 e f^{(n-1)}(\xi) \geq 0. Entrambe le situazioni contraddicono l’equazione \eqref{eq3769:1}.
Se n=2 abbiamo nuovamente raggiunto la tesi, dal momento che dall’equazione \eqref{eq3769:2} segue che 0 è un minimo locale (il che dipende dalla scelta che abbiamo fatto, di porre f^{(n)}(0) > 0).
Se n>2, osserva che \eqref{eq3769:2} implica che f^{(n-3)}(x) è strettamente monotona in \mathcal N. Insieme all’ipotesi f^{(n-3)}(0) = 0, questo implica \frac{f^{(n-3)}(x)}{x} > 0per ogni x \in \mathcal N \setminus \{0\}.
A questo punto è immediato procedere iterativamente e mostrare che f^{(n-2k)}(x)>0 \ \ \mbox{per} \ \ k=0,1\dots ,\left\lfloor \frac{n}2\right\rfloor-1 per ogni x \in \mathcal N \setminus \{0\}, e che \frac{f^{(n-2k-1)}(x)}{x} > 0\ \ \mbox{per} \ \ k=0,1,\dots ,\left\lfloor \frac{n}2\right\rfloor-1 per ogni x \in \mathcal N \setminus \{0\}. La tesi consegue da queste due ultime equazioni.
Ecco alcuni interessanti esempi. Il primo è estratto da “Numbers and Functions” di Robert Burn. Consideraf(x) = \begin{cases}x + 2x^2 \cos\left(\frac1{x}\right) & (x\neq 0) \\ 0 & (x=0).\end{cases} Questa funzione ha la derivata prima in 0 uguale a 1 (usa la definizione di derivata!). Tuttavia f(x) non è crescente in alcun intorno di 0. Per esercizio puoi dimostrare infatti che f\left(\frac1{2k\pi}\right) > f\left(\frac1{(2k-1)\pi}\right) per ogni k =1,2,\dots. Osserva infine che f'(x) non è continua in 0.
L’esempio precedente può essere generalizzato usando la funzionef(x) = \begin{cases}\frac{ax^n} {n!} + x^{2n}\cos\left(\frac1{x}\right) & (x\neq 0)\\ 0 & (x=0),\end{cases}dove f^{(k)}(0) = 0 per 0<k<n e f^{(n)}(0) = a, con f^{(n)}(x) non continua in 0.
Nota che l’enunciato del Teorema richiede che esista almeno una derivata non nulla.
Se tutte le derivate in c fino all’ordine n-1 esistono e sono uguali a 0, e la derivata n-esima in c non esiste, non si può trarre alcuna conclusione sull’esistenza o meno di un massimo/minimo locale. Considera ad esempio f(x) = \begin{cases} x^{2(n-1)}\left[2 + \cos \left(\frac1{x}\right)\right] & (x\neq 0) \\ 0 & (x=0). \end{cases}\tag{3}\label{eq3769:3}Questa funzione, per ogni n>1, ha un minimo (globale) in 0, ha derivata k-esima f^{(k)}(0) = 0 per 0<k<n, mentre f^{(n)} (x) non è definita in 0 (vedi figura qui sotto).
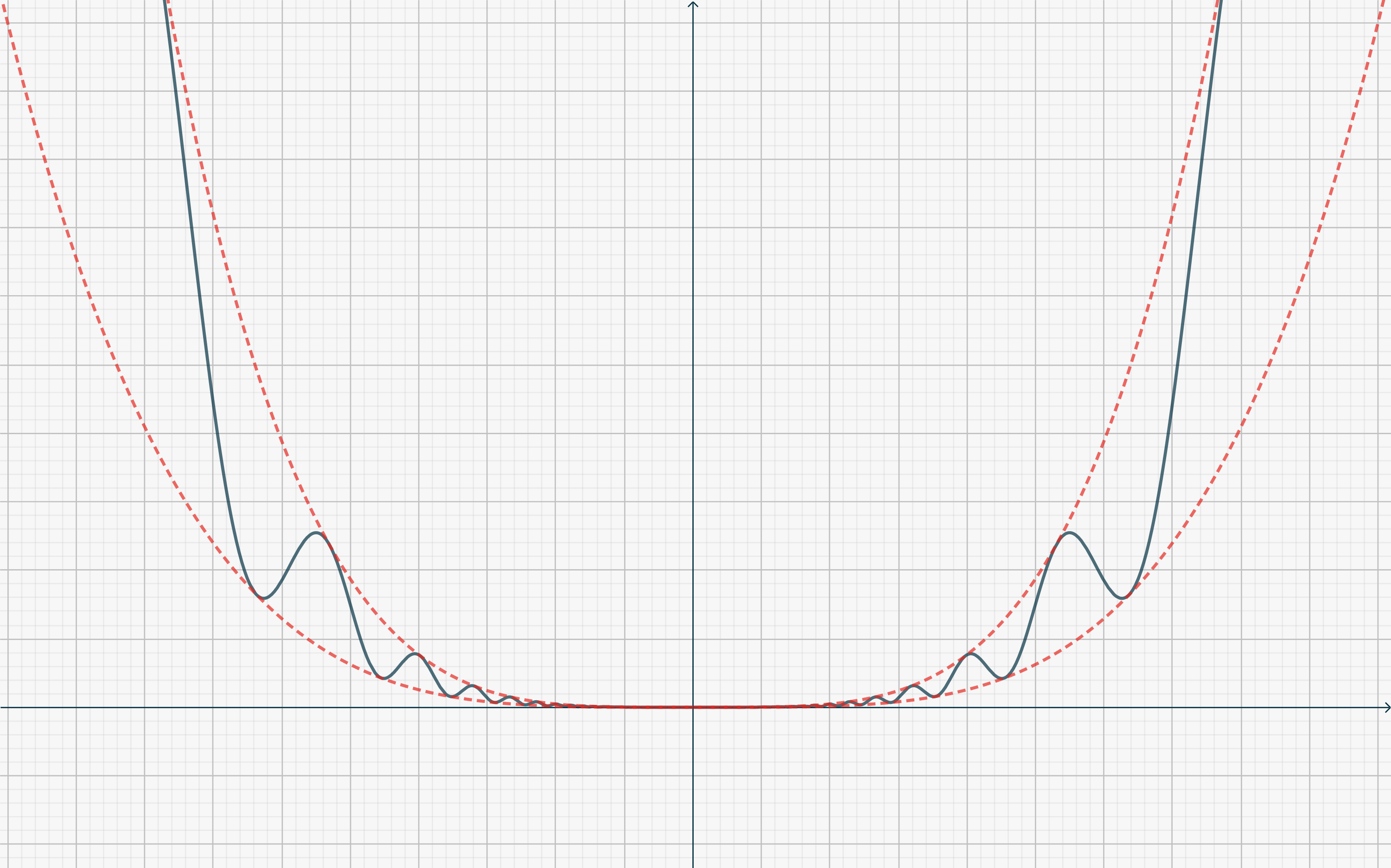
Esercizio proposto.
- Mostra che, per x \neq 0, la derivata della funzione \eqref{eq3769:3} può essere maggiorata come segue.f'(x) \leq x^{2n-4}\sin\left(\frac1{x}\right) + 6(n-1)x^{2n-3}.
- Deduci che per x = \frac1{2k\pi -\frac{\pi}2}, con k intero e k>\frac14 + \frac{3(n-1)}{\pi}, f'(x) è negativa.
- Concludi che f(x) non è monotona crescente in alcun intorno destro di 0.
In modo analogo, per n>1, la funzionef(x) = \begin{cases} x^{2n-1}\left[2 + \cos \left(\frac1{x}\right)\right] & (x\neq 0) \\ 0 & (x=0). \end{cases} (che non ha un punto di massimo o minimo in 0, essendo una funzione dispari) ha derivate nulle (e continue) in 0 fino all’ordine n-1, mentre la derivata n-esima in 0 non esiste. La situazione è schematizzata dalla Figura qui sotto.
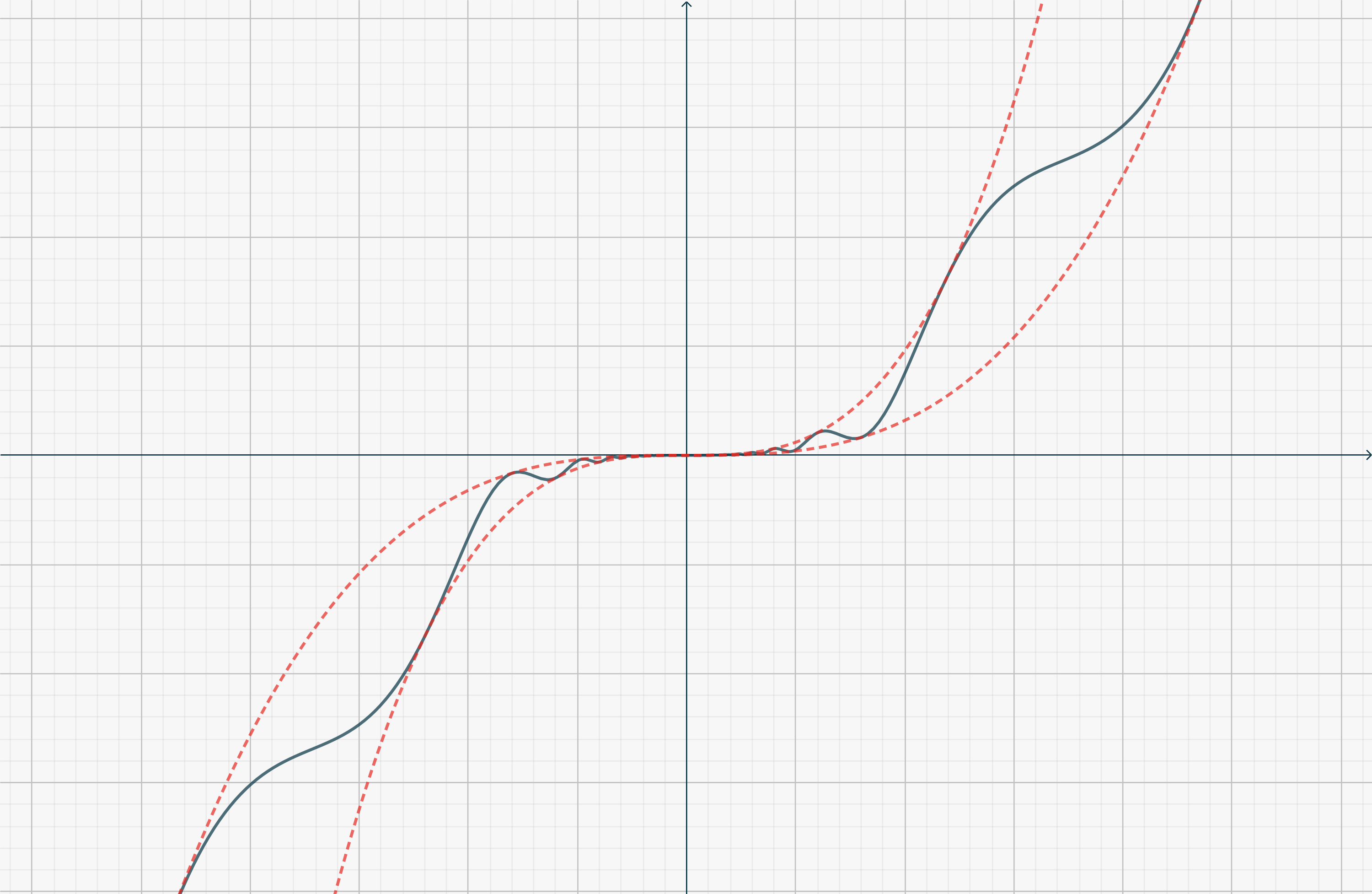
Per ragioni simili, se tutte le derivate sono nulle in c non si può trarre alcuna conclusione. Considera ad esempiof(x) = \begin{cases} e^{-\frac1{x^2}} & (x\neq 0) \\ 0 & (x=0),\end{cases}ef(x) = \begin{cases} \frac{x}{|x|}e^{-\frac1{x^2}} & (x\neq 0) \\ 0 & (x=0).\end{cases}
