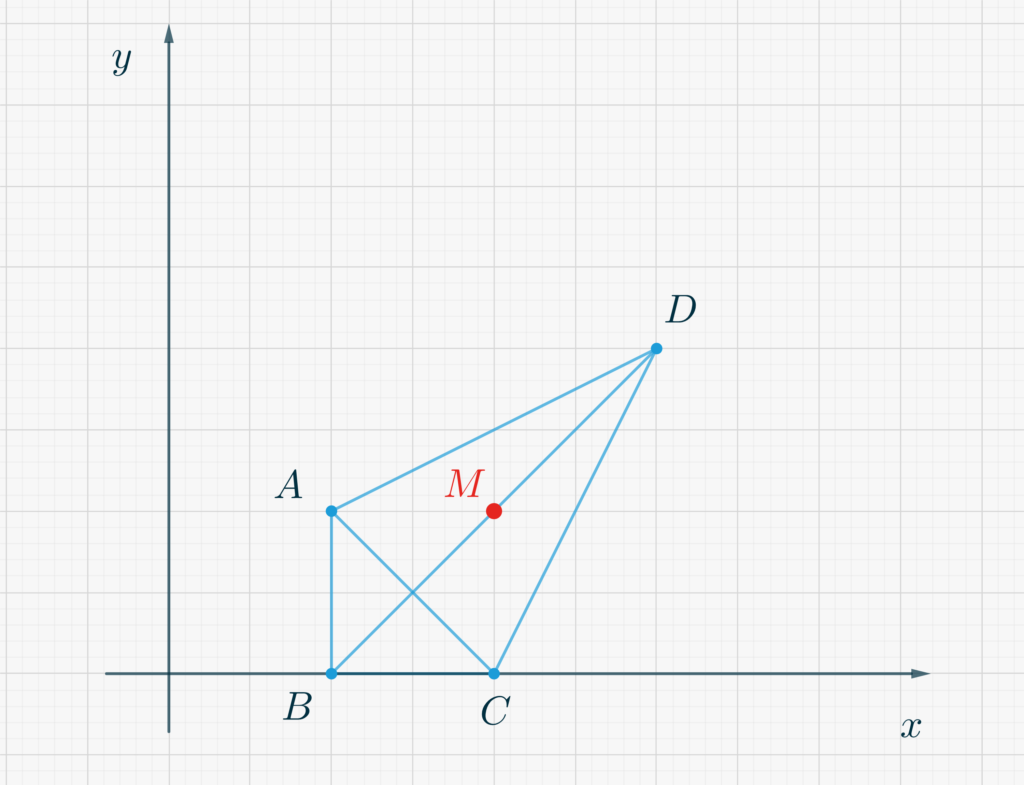
Get pen and paper and draw a cartesian plane. Then draw, on it, a set of points with integer coordinates, such as \(A(1,1)\), \(B(1,0)\), \(C(2,0)\), \(D(3,2)\), and so forth… Connect in all possibile ways these points with line segments and notice whether such segments intercept other integer coordinates points. For example, no interior point of \(CD\) has integer coordinates, while \(BD\) passes through point \((2,1)\). We want to understand what is the maximum number of points we can draw, so that the line segments connecting them do not pass through other points having integer coordinates (except, of course, the endpoints).
In the Figure below, the situation presented as an example has been depicted. The red dot marks the point \(M(2,1)\).
- It might be useful to first observe that in fact you can draw \(4\) points that satisfy the requirement. Which ones, for example?
- Thus, the problem becomes to understand if we can draw more than \(4\) points such that no line segments having these as endpoints passes through other points in the grid.
- This looks like too general a question. So you might want to concentrate only on the possibility that the midpoint may be an integer coordinate point or not. How do you calculate the coordinates of the midpoint of a line segment, having the coordinates of its endpoints?
- When is the sum of two integers even? When is it odd? Deduce the conditions that the coordinates of points, say, \(P(x_P,y_P)\) and \(Q(x_Q,y_Q)\) must satisfy so that the line segment connecting them does not have an integer coordinates midpoint.
- Divide the set of all integer coordinates points in the cartesian plane in \(4\) subsets according to the following rule: “two points are endpoints of a line segment whose midpoint has integer coordinates if and only if they belong to the same subset”.
- Deduce that the maximum number of points you can draw that satisy the requirement is \(4\).