Putnam competition questions have often represented for me a very good motivation to train and further develop my knowledge in real analysis. In this post I want to show you another example of this kind of experience.
Problem A.6 of 2020 Putnam competition goes like that.
For a positive integer \(N\), let \(f_N\) be the function defined by
\[f_N(x) = \sum_{n=0}^N \frac{N+1/2-n}{(N+1)(2n+1)} \sin((2n+1)x).\tag{1}\label{3985:1}\]
Determine the smallest constant \(M\) such that \(f_N(x) \leq M\) for all \(N\) and all real \(x\).
As a first step, I did what I often recommend to my students, that is I tried to acquaint myself with the situation by analyizing a few base cases. I therefore studied \(f_1(x)\) and \(f_2(x)\), which are pretty easy to deal with, and noted that in both cases the derivative contains a factor \(\cos x\) and some other non negative factor, hinting at a global maximum at \(x=\pi/2\). I suggest you to do the same and check that \[f’_1(x) = \cos x \cdot \cos^2 x\] and \[f’_2(x) = \frac16\cos x (4\cos^2 x-1)^2.\]
Generalizing this result took me some time since the the general expression for the derivative of \(f_N(x)\), i.e. \[f’_N(x) = \frac1{2(N+1)}\sum_{n=0}^N(2N+1-2n)\cos((2n+1)x),\] though somehow neat, is not easy to factor.
Thats is why I decided to represent the same expression in the complex domain, hoping for some simplification. You get \[f’_N(x)=\frac1{2(N+1)}\Re\left\{e^{jx}\sum_{n=0}^N(2N+1-2n)e^{j2nx}\right\}.\]Some manipulations get you to a geometric sum and the derivative of the same geometric sum. More precisely\begin{eqnarray}f’_N(x) &=& \frac1{2(N+1)}\Re\left\{(2N+1)e^{j(N+1)x}\cdot\frac{\sin((N+1)x)}{\sin x}+\right.\\
&+ &\left.je^{jx}\frac{d}{dx}\left(e^{jNx}\
\cdot \frac{\sin((N+1)x)}{\sin x}\right)\right\},
\end{eqnarray}valid for \(x\neq k\pi\). Fill in the steps the take you from here to \[f’_N(x)= \frac{\cos x\sin^2((N+1)x)}{2(N+1)\sin^2 x}, \ \ \mbox{for}\ \ x\neq k\pi.\tag{2}\label{3985:2}\]The function in \eqref{3985:2} has removable discontinuities in \(x=k\pi\) so you can easily determine the derivative at those points, by taking the limit (this is also left as an exercise). The above expression confirms the intuition that for all \(x\in \mathbb R\) \[f_N(x) \leq f_N\left(\frac{\pi}2\right).\]
Hopefully the sequence \(f_N(\pi/2)\) is monotonically increasing and convergent, in which case \(M\) is precisely its limit. Let us find out!
Luckily the sine term in the sum \eqref{3985:1} simply gives a \((-1)^n\) contribution in \(x=\pi/2\), so that, after some manipulation we get to\[f_N\left(\frac{\pi}2\right) = \begin{cases}S_N & (N \ \ \mbox{odd})\\ S_N -\frac1{2(N+1)}& (N \ \ \mbox{even}).\end{cases},\]where \[S_N = \sum_{n=0}^N \frac{(-1)^n}{2n+1} \stackrel{N\to\infty}{\to} \frac{\pi}4.\] Convergence is thus proved. We need monotonicity to conclude that \(M = \pi/4\). Notice that\begin{eqnarray}
f_{2N+1}(\pi/2) &=& S_{2N+1} = S_{2N} -\frac1{4N+3}>\\ &>&S_{2N}-\frac1{4N+2}=f_{2N}(\pi/2),
\end{eqnarray}and that and that\begin{eqnarray}f_{2N}(\pi/2) &=& S_{2N} – \frac1{4N+2} = S_{2N-1} + \frac1{4N+1}-\frac1{4N+2}>\\ &>&S_{2N-1}=f_{2N-1}(\pi/2),\end{eqnarray}which completes the proof.
If you determined the derivative at \(x=k\pi \) you might have noticed that those values diverge when \(N\to \infty\). On the other hand, for any \(\overline x \neq k\pi\) \[\lim_{N\to \infty}f’_N(\overline x) = 0.\tag{3}\label{3985:3}\]This suggests that the sequence of functions \(f_N(x)\) converges (pointwise) to a piecewise constant function. The plot of \(f_N(x)\) for the first few values of \(N\) hints at the same direction.
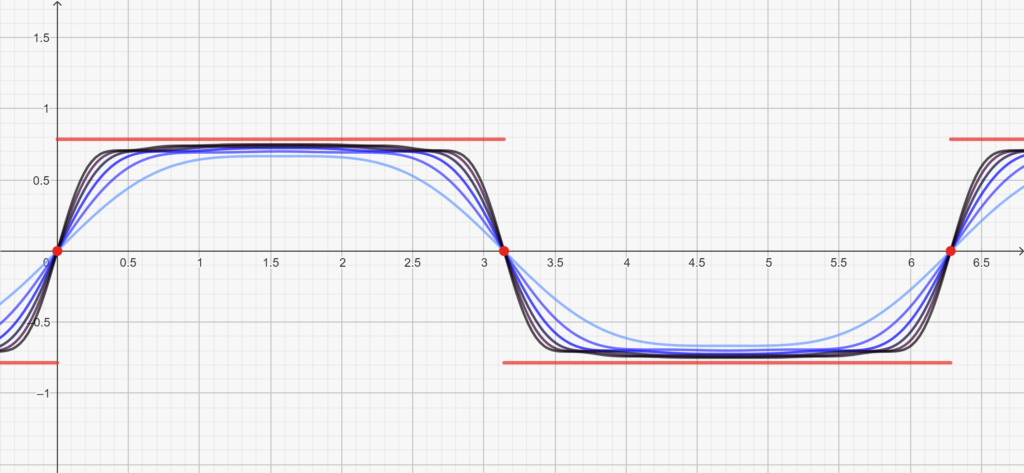
We want therefore to complete the exercise by proving that \[f_N(x) \to f(x)= \begin{cases}(-1)^k \frac{\pi}4 & (k\pi < x < (k+1)\pi \\ 0 & (x=k\pi).\end{cases}\]We could approach the proof using \eqref{3985:1} and Fourier analysis, but the same result can be obtained with more rudimentary instruments.
- The simmetries of the functions involved allow us to work in the interval \([0,\pi/2]\) only. First check convergence in \(x=0\), and in \(x=\pi/2\).
- Suppose by contradiction that there exists \(0< \overline x<\pi/2\) such that \(f_N(\overline x) \not \to \pi/4\). Use the definition of limit to construct a sequence \(f_{n_k}(\overline x)\), \(k=1,2,\dots\), such that\[\left|f_{n_k}(\overline x)-\frac{\pi}4\right|>\varepsilon.\]for some fixed \(\varepsilon>0\).
- Use 1. to prove that, for large enough \(k\),\[\left|f_{n_k}\left(\frac{\pi}2\right) – \frac{\pi}4\right|< \frac{\varepsilon}2.\]
- We can now put 2. and 3. together to show that \begin{eqnarray}
\left|\frac{f_{n_k}(\overline x)-f_{n_k}(\pi/2)}{\overline x -\pi/2}\right| &=& \left|\frac{f_{n_k}(\overline x)-\pi/4 + \pi/4- f_{n_k}(\pi/2)}{\overline x -\pi/2}\right|\geq \\
&\geq&\left|\frac{|f_{n_k}(\overline x)-\pi/4| – |f_{n_k}(\pi/2)-\pi/4|}{\overline x -\pi/2}\right|>\frac{\varepsilon}{\pi},
\end{eqnarray}for large enough \(k\). - Use Mean Value Theorem and 4. to prove the existence of a point \(\overline x < \xi_k< \pi/2\) such that \[f’_{n_k}(\xi_k) > \frac{\varepsilon}{\pi}.\]
- We need now a condition on the derivative contradicting 5. Observe first that \eqref{3985:3} is not enough. Why? Use \eqref{3985:2} to show that for any given \(x\) such that \(0<\overline x<x<\pi/2\)\[f’_N(x) \leq\frac1{2(N+1)\sin^2\overline x}.\]
- Show that 6. contradicts 5., thus completing the proof of pointwise convergence.
