As we have seen in another post, identities involving inverse tangent look much less mysterious if analyzed from a purely geometrical perspective. Here you have the chance to further practice on the subject and to demonstrate a more general formula. Let’s start with the relationship
\begin{equation}\arctan x + \arctan\left(\frac{x+1}{x-1}\right) =\frac{3\pi}{4}, \ \ \mbox{for}\ \ x>1.\tag{1}\label{eq630:1}\end{equation}
We will start again with the now ubiquitous right-angled triangle \(\triangle ABC\) with sides \(\overline{AB} = 1\), \(\overline{BC} = x\), and hypothenuse \(\overline{AC} = \sqrt{1+x^2}\).
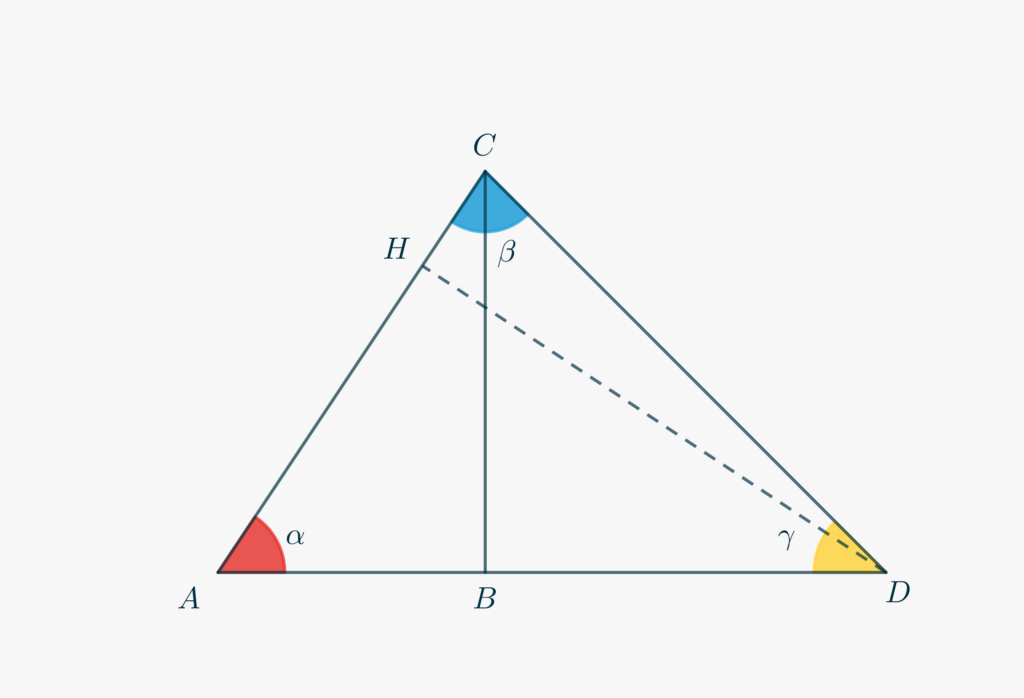
- Extend \(AB\) with a segment \(\overline{BD} = x\).
- Triangle \(\triangle BCD\) is isosceles. What can you say, then, about the angle \(\gamma = \angle ADC\)?
- Use what you observed, and the fact that the sum of the interior angles of \(\triangle ACD\) is \(\pi\), to write a relationship connecting \(\alpha\) and \(\beta\). You should get \[\beta = \frac{3\pi}{4}-\alpha.\]
- Draw from \(D\) the line perpendicular to \(AC\), that intersects \(AC\) in \(H\).
- \(\triangle ABC\) and \(\triangle ADH\) are similar. Why?
- From the scale factor between these triangles and the fact that \(\overline{AD} = 1+x\), determine \(\overline{DH}\), \(\overline{AH}\), and finally \(\overline{CH} = \overline{AC}-\overline{DH}\).
- Write down \(\beta\) as \(\arctan\left(\frac{\overline{DH}}{\overline{CH}}\right)\).
- Use the relationship found in 3. to get your final result.
If you followed without difficulties the previous demonstration, you should now be able to prove also the following identity.
\begin{equation}\arctan x + \arctan\left(\frac{\sqrt 3 x+1}{x-\sqrt 3}\right)=\frac{5\pi}{6}, \ \ \mbox{for} \ \ x >\sqrt 3.\tag{2}\label{eq630:2}\end{equation}
It is just a matter of modifying the measure of the angle \(\gamma\), and make it equal to \(\frac{\pi}{6}\). What is then the measure of \(\overline{BD}\)? Recall that \(\frac{\pi}{3}\) is the measure of the interior angles of an equilateral triangle. Procede from here as you have done before, in order to prove \eqref{eq630:2}.
You might be wondering now whether the expressions \eqref{eq630:1} and \eqref{eq630:2} can be further generalized. After all \(\gamma\) can be arbitrarily chosen, and in general we would have \(\overline{BD} = \frac{x}{\tan\gamma}\). Viceversa, if we take \(\overline{BD} = \frac{x}{y}\), we will get \(\gamma = \arctan y\).
Use the latter notation and generalize the procedure that you adopted so far. Recalling that
\[\beta = \pi – \arctan x – \arctan y,\]
obtain the following identity
\[\arctan x + \arctan y = \pi – \arctan\left(\frac{x+y}{xy-1}\right),\]
which is valid for \(x>\frac{1}{y}>0\).