Questo articolo è dedicato a un importante teorema di geometria che viene attribuito all’astronomo greco Menelao di Alessandria. Il teorema è relativo ai rapporti tra le lunghezze dei segmenti ottenuti “tagliando” i lati di un triangolo (o i suoi prolungamenti) con una retta che non passi per i suoi vertici. Il suo utilizzo consente di risolvere rapidamente anche problemi piuttosto complessi, che, altrimenti, richiederebbero l’utilizzo di nozioni di tipo trigonometrico.
Teorema. Sia dato un triangolo \(\triangle ABC\) e una retta non passante per i vertici del triangolo; siano inoltre \(D\), \(E\) e \(F\) le sue intersezioni con i (prolungamenti dei) lati \(BC\), \(AC\) e \(AB\) rispettivamente, allora si ha
\begin{equation}\frac{\overline{AF}}{\overline{FB}}\cdot \frac{\overline{BD}}{\overline{DC}}\cdot \frac{\overline{CE}}{\overline{EA}} = 1.\tag{1}\label{eq749:1}\end{equation}
Il teorema, nella sua versione più completa, mostra in realtà che la condizione \eqref{eq749:1} è necessaria e sufficiente affinché la terna di punti sia allineata. La sua dimostrazione è molto semplice e si basa esclusivamente sui rapporti di similitudine di alcuni triangoli ausiliari.
Vediamo una prima semplicissima applicazione del teorema nel seguente esercizio di “riscaldamento”
Dato un triangolo \(\triangle ABC\), conduci da \(A\) una retta che interseca \(BC\) in \(D\) e da \(B\) una retta che interseca \(AC\) in \(E\). Sia \(P\) il punto di intersezione tra queste due rette. Sapendo che l’area di \(\triangle ABP\) è uguale a \(6\), quella di \(\triangle AEP\) è \(3\) e quella di \(\triangle BDP\) è \(4\), determinare l’area del quadrilatero \(CDPE\).
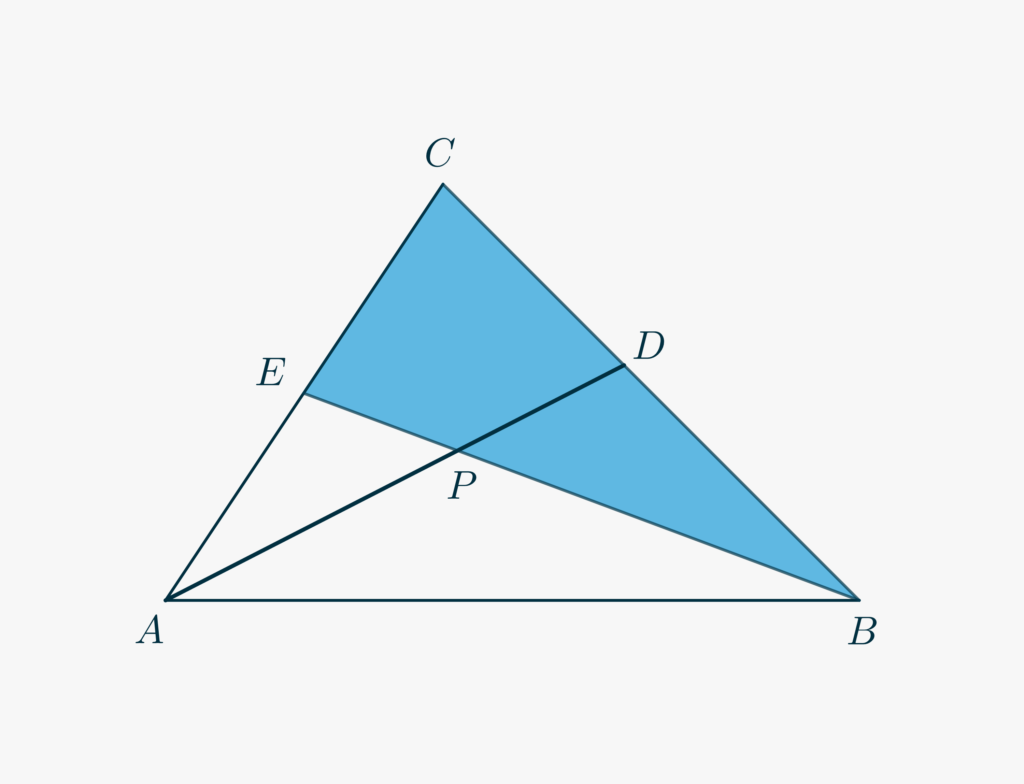
- Chiama \(x\) l’area incognita del quadrilatero \(CEPD\).
- Per determinarla usiamo il teorema di Menelao, applicandolo al triangolo \(\triangle BEC\), tagliato dalla retta \(AD\). Sappiamo quindi che \begin{equation}\frac{\overline{EP}}{\overline{PB}}\cdot\frac{\overline{BD}}{\overline{DC}}\cdot\frac{\overline{AC}}{\overline{AE}}=1.\tag{2}\label{eq749:2}\end{equation}
- Dobbiamo quindi esprimere il primo membro di \eqref{eq749:2} in funzione di \(x\).
- Usando il rapporto tra le aree di \(\triangle ABP\) e di \(\triangle AEP\), verifica che \(\frac{\overline{EP}}{\overline{PB}} =\frac{1}{2}\).
- Con la stessa strategia, e usando il fatto che l’area di \(\triangle ABD\) è pari a \(10\) e quella di \(\triangle ADC\) è \(3+x\), scrivi in funzione di \(x\) il rapporto \(\frac{\overline{BD}}{\overline{DC}} \).
- Procedi come nel punto precedente con le aree di \(\triangle ABC\) e \(\triangle ABE\) per determinare in funzione di \(x\) il rapporto \(\frac{\overline{AC}}{\overline{AE}}\).
- Concludi risolvendo l’equazione rispetto a \(x\); troverai \(x = \frac{19}{2}\).
Siamo pronti per affrontare il prossimo esercizio, più articolato, che mette in evidenza l’efficacia del metodo, in alternativa ad approcci basati sulla geometria analitica e la trigonometria.
Dato il triangolo equilatero \(ABC\) e un punto \(P\) sul cerchio ad esso circoscritto, siano \(D\), \(E\) e \(F\) i punti di intersezione, rispettivamente, di \(PA\) con la retta \(CB\), di \(PB\) con la retta \(AC\) e di \(PC\) con la retta \(AB\). Dimostrare che l’area di \(DEF\) è doppia di quella di \(ABC\).
Senza ledere le generalità del risultato, supponiamo \(P\) si trovi sul semipiano determinato da \(BC\) non contenente \(A\). Supponiamo inoltre sia \(\overline{AB} = 1\). Nel seguito useremo la notazione \([\cdots]\) per riferici all’area del poligono i cui vertici sono riportati tra quadre.
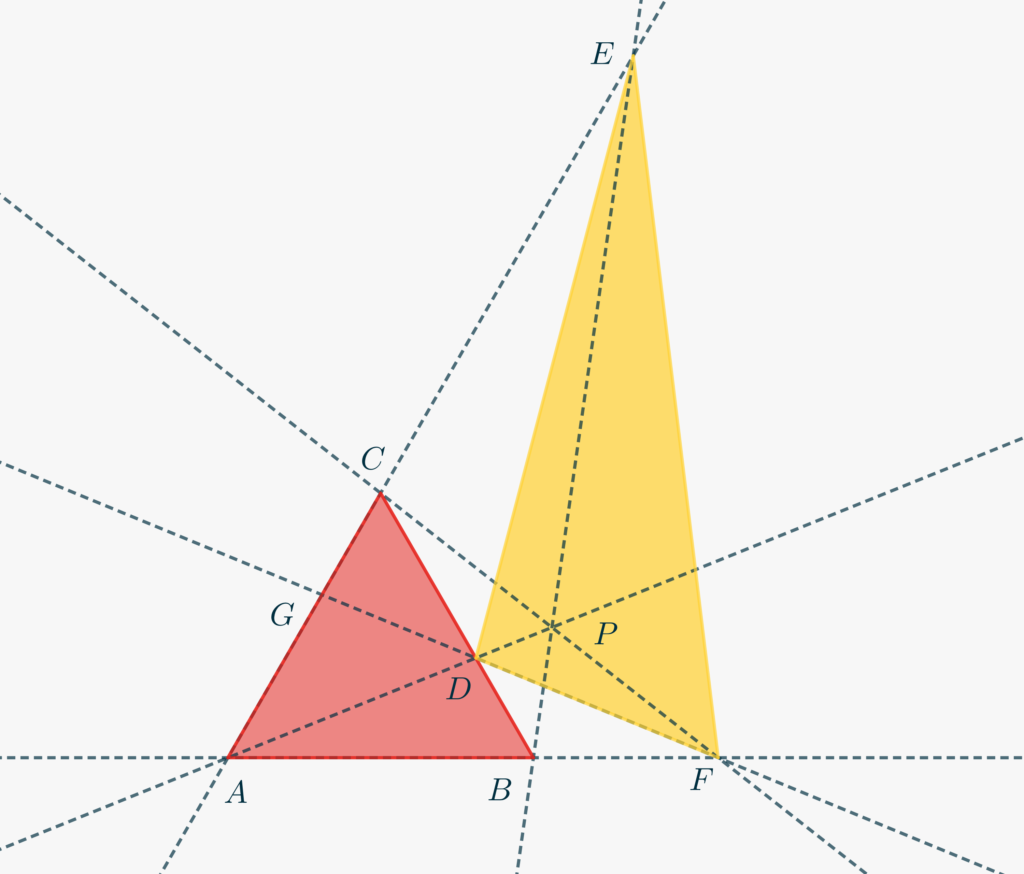
- Osserva che l’appartenenza di \(P\) al cerchio circoscritto al triangolo \(\triangle ABC\) è equivalente a fissare \(\angle CPB = 120°\). Per quale motivo?
- Denominiamo \(\overline{BF} = x\). Osserva che, una volta fissata la lunghezza di questo segmento, l’intera costruzione è determinata. L’obiettivo può diventare quello di esprimere \([DEF]\) in funzione di \(x\), e in modo da verificare che, in realtà si abbia \[[DEF] = 2[ABC],\] indipendentemente da \(x\).
- Concentrati in primo luogo sul triangolo \(\triangle BCF\), che è riportato qui sotto, per facilitarti nelle dimostrazioni seguenti.
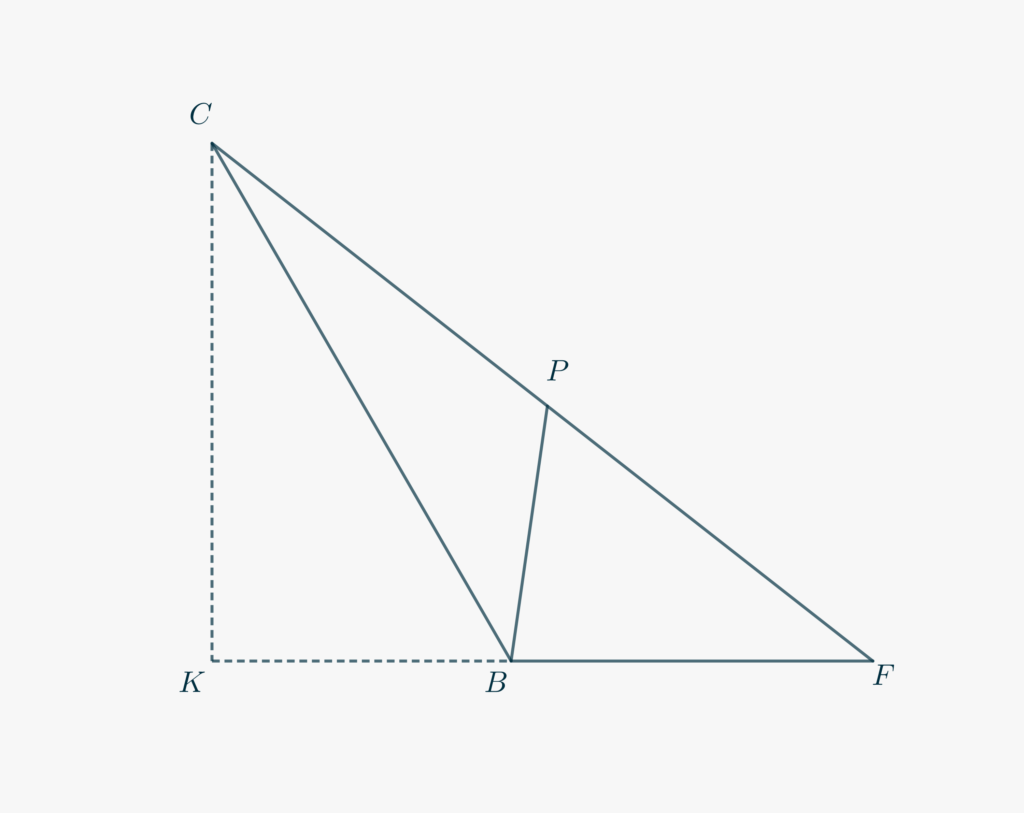
- Dimostra che i triangoli \(\triangle BCP\) e \(\triangle BCF\) sono simili.
- Ricordando che \(\overline{BC} = 1\) e \(\overline{BF} = x\), fai uso della similitudine per dimostrare che \begin{equation}\overline{CP}\cdot\overline{FC}= 1.\tag{3}\label{eq749:3}\end{equation}
- Osserva che \(\triangle CKB\) è metà di un triangolo equilatero. Deducine le lunghezze di \(\overline{CK}\) e \(\overline{KF}\).
- Usa il teorema di Pitagora per calcolare la lunghezza di \(FC\). Dovresti ottenere \[\overline{FC} = \sqrt{x^2+x+1}.\]
- Ricorri infine alla relazione \eqref{eq749:3} per calcolare \[\overline{CP}= \frac{1}{\sqrt{x^2+x+1}}\] e \[\overline{FP} = \frac{x(x+1)}{\sqrt{x^2+x+1}}.\]
- Ora possiamo tornare alla Figura iniziale, per applicare ripetutamente il teorema di Menelao. Applicalo al triangolo \(\triangle ACF\) tagliato dalla retta \(BE\), per ricavare \[\frac{\overline{CE}}{\overline{AE}} = \frac{1}{x+1}.\] Sapendo che \(\overline{AE} – \overline{CE} = 1\), determina \(\overline{AE} = \frac{1}{x}\) e \(\overline{CE} = \frac{x+1}{x}\).
- Utilizza ancora il teorema sul triangolo \(\triangle BFC\) e tagliato da \(AP\), unitamente all’informazione \(\overline{BD}+\overline{CD}=1\), per ricavare le lunghezze di \(\overline{CD}\) e \(\overline{BD}\). Otterrai \(\overline{CD} = \frac{1}{x+1}\) e \(\overline{BD} = \frac{x}{x+1}\).
- Ancora con il teorema di Menelao, stavolta sul triangolo \(\triangle ABC\) tagliato da \(FG\), e utilizzando la relazione \(\overline{AG} + \overline{CG} = 1\), ricava \(\overline{AG} = \frac{x+1}{x+2}\) e \(\overline{CG} = \frac{1}{x+2}\).
- Un’ultima applicazione del teorema, al triangolo \(\triangle CGF\) tagliato da \(AP\), ti permette di determinare il rapporto \[\frac{\overline{GD}}{\overline{DF}} = \frac{1}{x(x+2)}.\]
- Per concludere, seguendo a ritroso il procedimento usato nell’esercizio di “riscaldamento”, determiniamo ora il rapporto tra le aree usando triangoli con un’altezza in comune e basi che hanno tra loro un rapporto noto, calcolato nei passaggi precedenti. Puoi iniziare con l’area del triangolo \(\triangle ACF\) che ha in comune con \(ABC\) l’altezza relativa ad \(AF\). Ricaverai quindi \[[ACF] = [ABC](1+x).\]
- Ora puoi ricavare l’area di \(\triangle AFE\), che ha in comune con \(\triangle ACF\), l’altezza relativa ad \(AE\), quindi \[[AFE] = [ACF] \cdot \frac{\overline{AE}}{\overline{AC}}.\] Controlla che questo ti dia \[[AFE] = [ABC]\cdot \frac{(x+1)^2}{x}.\]
- I due triangoli \(\triangle GFE\) e \(\triangle AFE\) hanno in comune l’altezza relativa alla base \(GE\). Ricavane il rapporto tra le aree e, quindi, la relazione \begin{equation}[GFE] = [ABC]\cdot\frac{2(x+1)^2}{x(x+2)}.\tag{4}\label{eq749:4}\end{equation}
- Da ultimo osserva che \begin{equation}\frac{[DFE]}{[GDE]} = \frac{\overline{GD}}{\overline{DF}} = \frac{1}{x(x+2)}\tag{5}\label{eq749:5}\end{equation} e che \begin{equation}[DFE] + [GDE] = [GFE]\tag{6}\label{eq749:6}.\end{equation} Sostituisci allora la \eqref{eq749:4} nella \eqref{eq749:6}. Da quest’ultima equazione, ricava \([GDE]\) e sostituiscilo nella \eqref{eq749:5}. Otterai un’equazione nella sola incognita \([DEF]\), la cui soluzione, come richiesto, è \[[DEF] = 2[ABC].\]
