Gli apparenti paradossi dell’infinito possono aiutarci a costruire una funzione iniettiva \(f(x)\) che sia definita in un intervallo chiuso e limitato, derivabile in \(a\), ma tale per cui la sua inversa \(f^{-1}\) non sia continua in \(f(a)\)?
Supponiamo per semplicità che \(a = 0\), \(f(0) = 0\) e\(f'(0) = 1\). L’obiettivo a appare a prima vista impossibile: perché la funzione sia derivabile in \(0\), con \(f'(0) = 1\), occorre che, per \(x\) abbastanza vicine all’origine, le immagini di \(x\) si “schiaccino” sulla bisettrice \(y=x\). E ciò sembra comportare che anche la funzione inversa in \(0\) sia per lo meno continua, se non addirittura derivabile.
Si potrebbe inoltre essere fuorviati dalla nota relazione
\begin{equation}\left( f^{-1}\right)'(f(x))=\frac1{f'(x)}\end{equation}
che, tuttavia, è applicabile se è noto a priori che la funzione inversa è derivabile, oppure se la derivata di \(f(x)\) è continua in un intorno di \(x\).
Cerchiamo di indagare meglio sulla richiesta. Vogliamo che \(f^{-1}\) non sia continua in \(f(0) = 0\), ovvero deve esistere \(\varepsilon>0\) tale per cui, per ogni \(\delta >0\), esiste \(x\), con \(|x| < \delta\),per la quale \(|f^{-1}(x)|\geq \varepsilon\).
Se traduciamo questa affermazione in una condizione su \(f\) otteniamo quanto segue. Esiste \(\varepsilon > 0\) tale per cui, per ogni \(\delta > 0\) possiamo trovare una \(|x|\geq \varepsilon\) che dia \(|f(x)| < \delta\). In altre parole, vogliamo che \(f(x)\) assuma valori arbitrariamente piccoli, per \(x\) ‘sufficientemente grandi’, la qual cosa non è in contraddizione con le ipotesi. L’aspetto più difficile della richiesta sembra essere quello di mantenere, nonostante tutto, l’iniettività della funzione.
A questo punto ci viene in aiuto il famoso paradosso dell’Albergo Infinito. Invece di accogliere un maggior numero (addirittura un numero infinito) di ospiti in un albergo infinito, già completamente occupato, vogliamo creare un numero infinito di discontinuità eliminabili in una funzione iniettiva (mantenendone l’iniettività) in modo tale da far sì che la funzione inversa non sia continua.
Ricorda infatti che una funzione continua in un intorno di \(0\) o è monotona (nel qual caso anche l’inversa è continua) oppure non lo è (e in questo caso la funzione non è iniettiva!). Quindi la funzione che vogliamo costruire deve essere continua (e derivabile) in \(0\) ma deve essere discontinua in un qualunque intorno di \(0\).
Ci concentriamo anzitutto sull’intervallo \([0,1]\). Una volta risolto il problema in intorni destri di \(0\), è facile ottenere una funzione definita in \([-1,1]\), per esempio mediante una simmetria. Partiamo dalla mappa \(g(x) = x\), che soddisfa le richiesta, salvo il fatto che la funzione inversa è in effetti continua in \(0\). Modificheremo quindi punto per punto questa mappa; per preservare la derivabilità in \(0\) faremo in modo che il grafico della funzione giaccia tra \(y=x\) e la parabola \begin{eqnarray} h(x) = -x^2+x.\end{eqnarray}
Introduciamo il primo ‘buco’ in \(x=\frac13\) ponendo \[g\left(\frac13\right)= h\left(\frac13\right)=\frac29.\]
In questo modo \(\frac13\) sarà utilizzato come immagine di qualche valore di \(x\) maggiore di \(\frac13\). Ora, però, per preservare l’iniettività dobbiamo liberare la ‘stanza’ che sarà occupata da \(\frac29\), il che ci obbliga a fissare \[g\left(\frac29\right) = h\left(\frac29\right) = h\circ h\left(\frac13\right) = \frac{14}{81}.\]
Possiamo procedere indefinitamente verso lo \(0\) imponendo ogni volta
\[g\left(h^{(n)}\left(\frac13\right)\right) = h^{(n+1)}\left(\frac13\right),\]
dove \[h^{(n)} (x) = \underbrace{h\circ h \circ \cdots \circ h}_n (x)\] per \(n>0\) e \(h^{(0)}(x) = x\).
Ciò che abbiamo fatto sinora garantisce che \(g\) sia ancora iniettiva per \(0\leq x< \frac13\). Possiamo riempire ora la ‘stanza’ liberata da \(\frac13\), per esempio fissando \[g\left(\frac23\right) = \frac13.\] La situazione è mostrata nella figura qui sotto, dove i cerchi gialli marcano alcune delle discontinuità che abbiamo introdotto. Il quadrato rosso evidenzia la difficoltà che dobbiamo gestire ora!
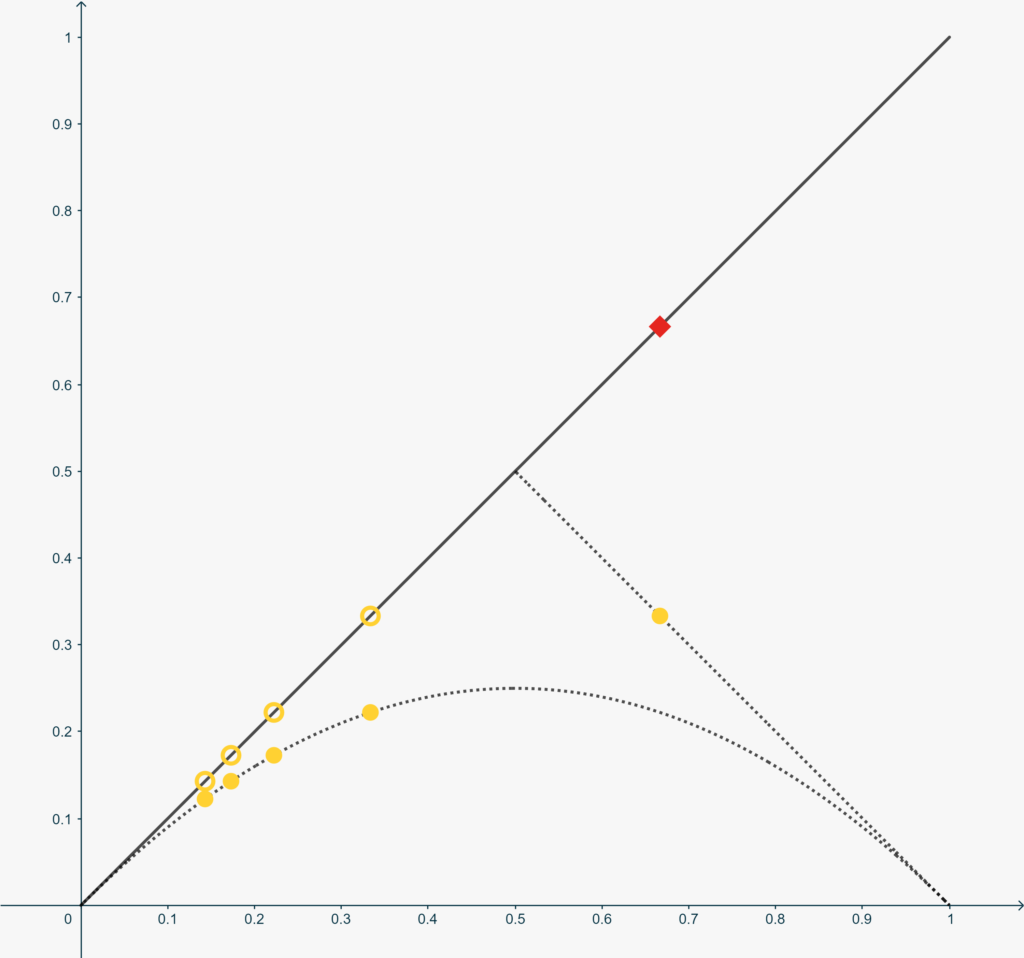
La simmetria parziale del grafico soprastante, però, suggerisce un modo di aggirare l’ostacolo. Disegniamo quindi la parabola di equazione \[x=y^2-y+1,\] il cui grafico è simmetrico di \(h(x)\) rispetto alla retta \[r: y=-x+1,\]anch’essa rappresentata qui sopra. Possiamo ‘spostare’ il quadrato rosso sulla nuova parabola ponendo \[g\left(\frac79\right) = \frac23.\]Ora ovviamente abbiamo lo stesso problema in \(x = \frac79\)… Ma possiamo procedere simmetricamente rispetto a quanto fatto negli intorni di \(0\). Il risultato, dopo alcuni passaggi, è rappresentato nella figura qui sotto.
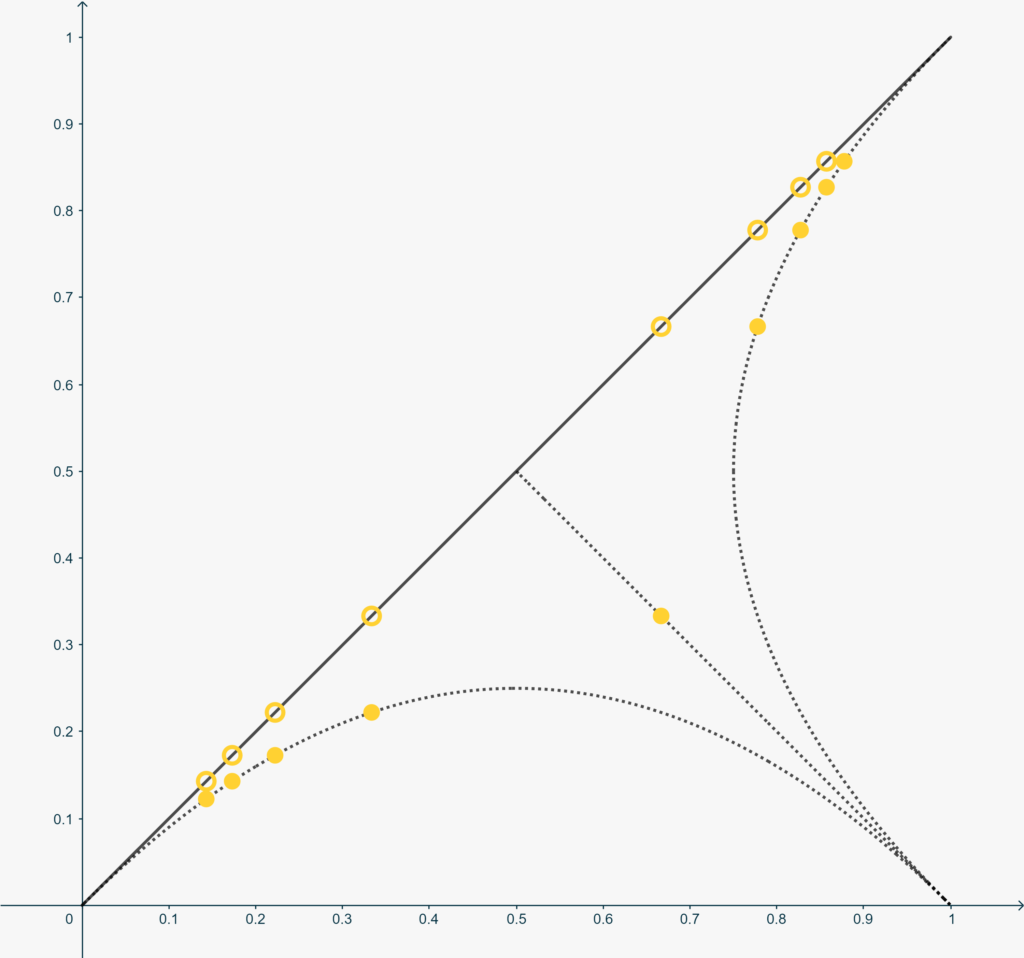
La funzione costruita finora è iniettiva in tutto l’intervallo ma la sua inversa è ancora continua in \(0\). Ora, però, possiamo ripartire con una nuova iterazione di ‘buchi’ partendo da \(\frac15\). Usando i reciproci dei numeri primi eviteremo che la nostra azione interferisca con quanto fatto nelle iterazioni precedenti. Infatti se \(p_k\) è la successione dei numeri primi, allora per \(n=0,1,2,\dots\) e per ogni \(p_k\), con \(k=1,2,\dots\), \[h^{(n)}\left(\frac1{p_k}\right) = \frac{m}{p_k^\ell}\] per un qualche intero positivo \(m\) e \(\ell\). Quindi per \(n\), \(k\) e \(h\) non contemporaneamente tutti uguali, \[h^{(n)}\left(\frac1{p_k}\right) \neq h^{(k)}\left(\frac1{p_h}\right).\]
Possiamo dare una definizione formale di \(g(x)\), definendo innanzitutto, per \(0\leq x \leq \frac12\), \[g_1(x)=
\begin{cases}
h(x) & \left(\mbox{se}\ \ x=h^{(n)}\left(\frac1{p_k}\right),\ \ \mbox{per qualche}\ k>1\ \mbox{e qualche}\ n\geq 0\right)\\
x & (\mbox{altrimenti}).
\end{cases}\]
Osserva che \(g_1(x)\) è iniettiva (qual è la sua immagine?). Possiamo quindi usare la simmetria rispetto a \(r\) e definire, per \(0\leq x \leq 1\),
\[g(x) = \begin{cases}
g_1(x) & \left(0\leq x\leq \frac12\right)\\
\frac1{p_k} & \left(\mbox{se}\ \ x=1-\frac1{p_k},\ \ \mbox{per qualche} \ k>1\right)\\
1-g_1^{-1}(1-x) & (\mbox{altrimenti}).
\end{cases}\]
In figura vedi un grafico approssimativo di \(g(x)\) dopo qualche iterazione su \(k\). Cerchi di colore diverso si riferiscono a differenti iterazioni sui reciproci dei numeri primi.
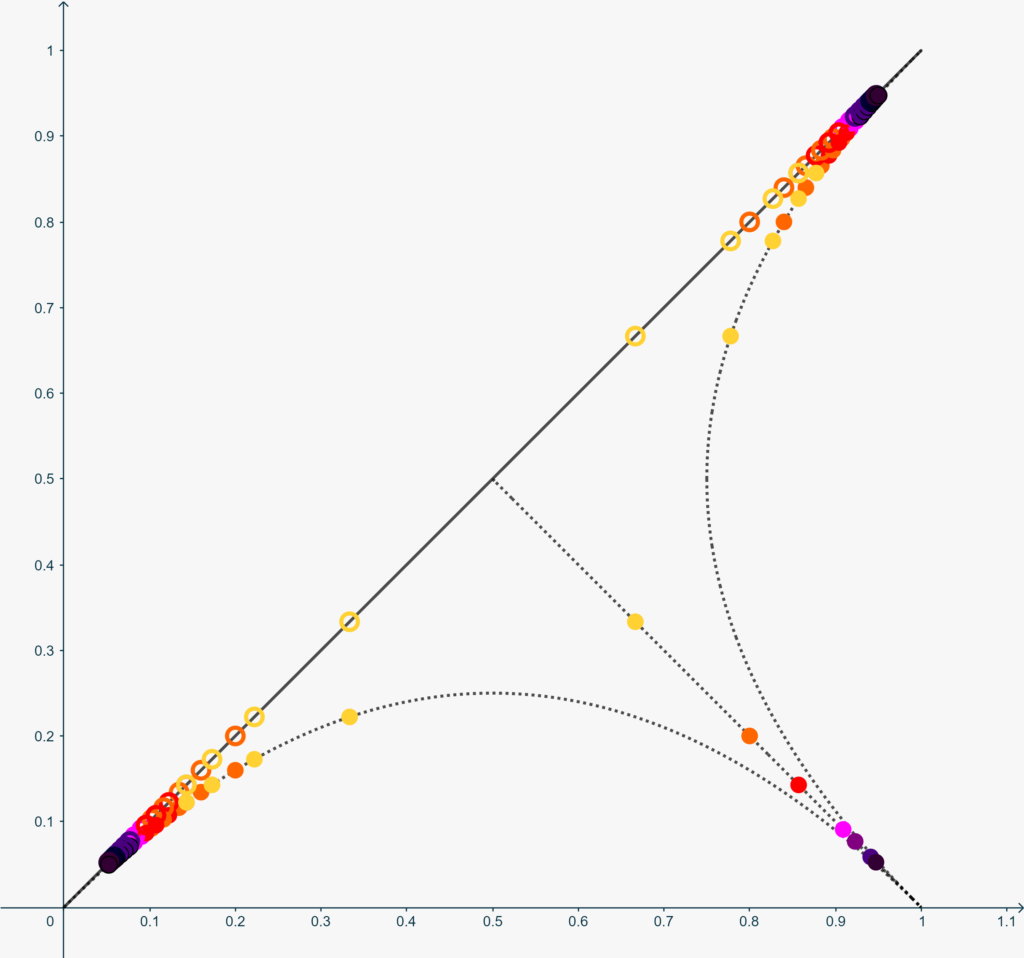
Se ora poniamo \[f(x) = \begin{cases} g(x) & (0\leq x \leq 1)\\ -g(-x) & (-1\leq x <0).\end{cases}\] abbiamo una funzione con le proprietà desiderate in \([-1,1]\).
Una nota finale. Osserva che \[\lim_{k\to \infty} \frac1{p_k} = 0,\]e che, per ogni \(k\),\[\lim_{n\to \infty} h^{(n)}\left(\frac1{p_k}\right) = 0.\] Di conseguenza ogni intorno di \(0\) non contiene solo un numero finito di discontinuità, ciò di elementi \(x\) tali per cui \(g(x) = h^{(n)}\left(\frac1{p_k}\right)\) for any \(n\) and \(k\). Pertanto, se \(\overline x \neq 0\) è un punto nel dominio di \(g\) tale per cui \(g(\overline x) = \overline x\), allora esiste \(\delta_{\overline x}>0\) tale che (g(x) = x\) per ogni \( x\in [\overline x-\delta_{\overline x}, \overline x + \delta_{\overline x}]\). Concludiamo che la funzione \(f\) è continua è differenziabile in ogni punto \(\overline x\) tale per cui \(g(\overline x) = \overline x\), cioè ovunque tranne che in una quantità numerabile di punti.
