Vogliamo mostrare un’altra applicazione del Teorema di Menelao, che, insieme ad un po’ di calcolo infinitesimale, ci porterà ad un risultato semplice e piuttosto sorprendente.
Considera un quadrato di lato \(1\) e dividi il lato di sinistra e quello inferiore in \(n\) segmenti uguali. Collega gli estremi di questi segmenti come indicato nelle Figure sottostanti (che mostrano i casi \(n=3, 5, 8\)). Vogliamo determinare quanto valga l’area ombreggiata al variare di \(n\) e, in particolare per \(n\to \infty\) (linea rossa nell’ultima Figura qui sotto). Infine calcoliamo la funzione il cui grafico è rappresentato dalla linea rossa.

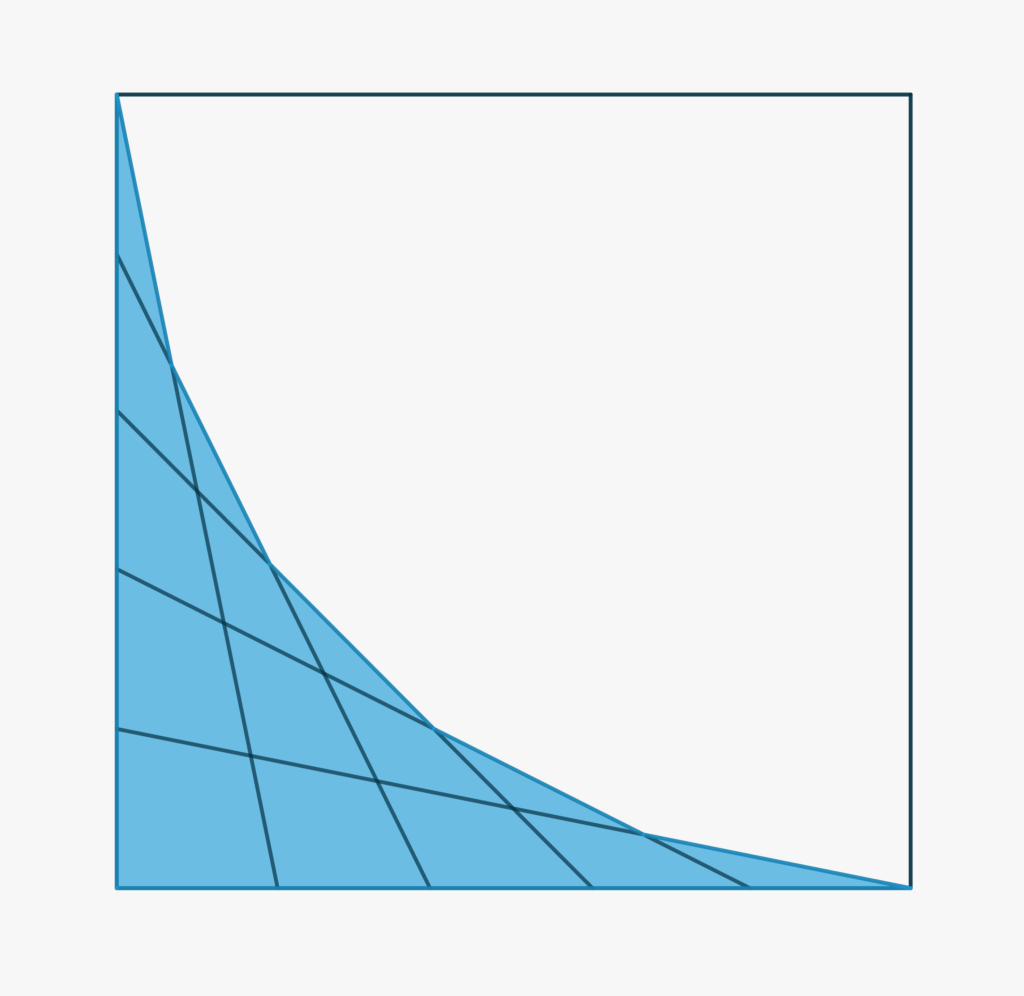
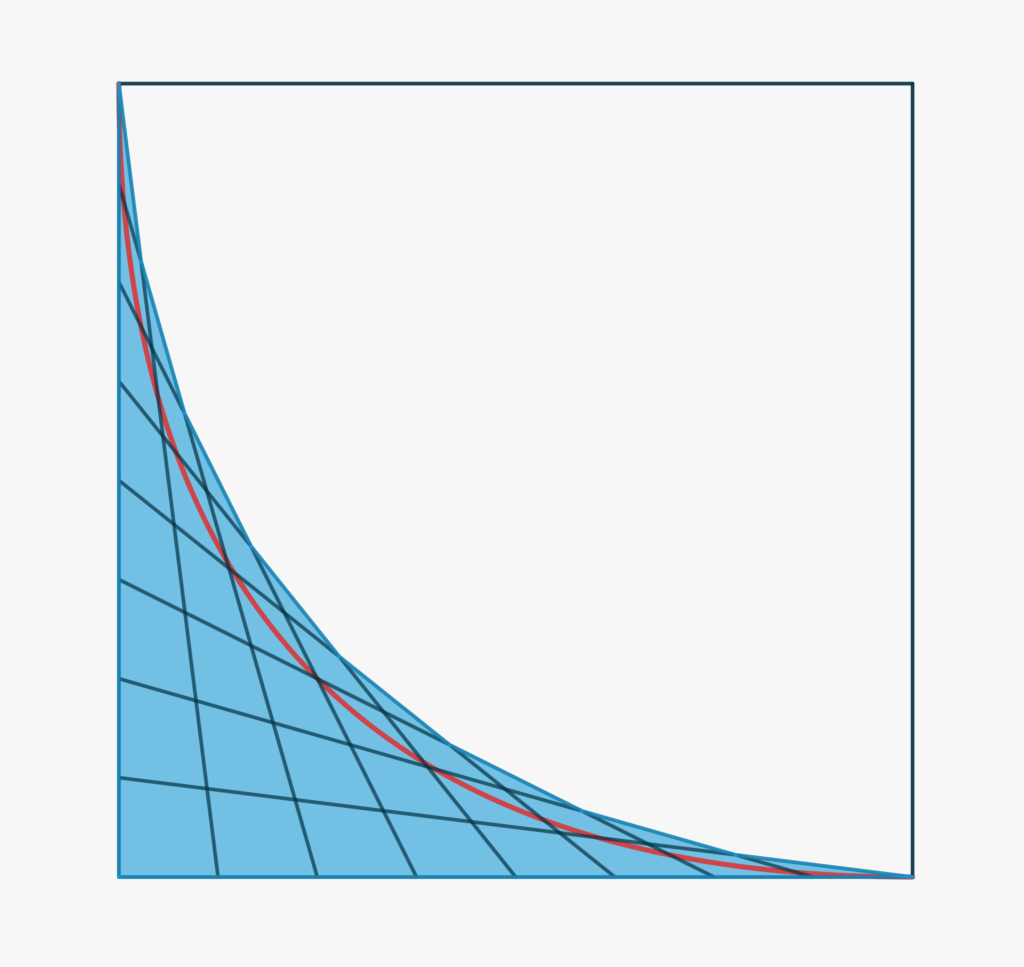
Potremmo approcciare il problema utilizzando la geometria analitica, ma è istruttivo ricorrere ancora una volta ai teoremi Geometria Euclidea.
A questo scopo, etichettiamo i punti del quadrato come mostrato nella Figura qui sotto per un generico valore di \(n\). Cerchiamo di determinare l’area richiesta sommando le aree dei triangoli \(\triangle A_iA_{i-1}C_i\), di cui due sono ombreggiati qui sotto.
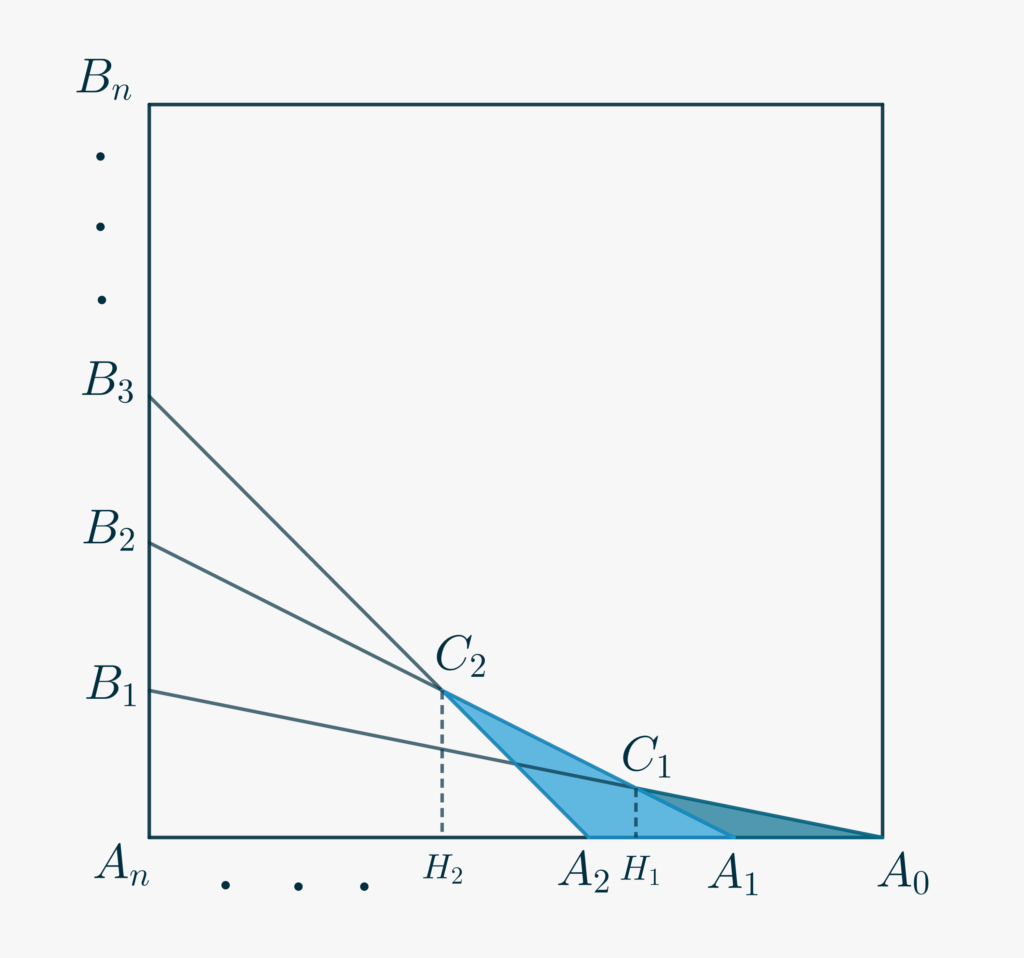
- Osserva che i triangoli considerati hanno tutti base \(\frac1{n}\) e che quindi ci occorre soltanto determinarne le altezze \(\overline{C_iH_i}\).
- Per \(i=1,2,\dots,n-1\), considera il triangolo \(\triangle A_nA_{i-1}B_i\) tagliato dalla linea \(\overline{A_iB_{i+1}}\). Applica il Teorema di Menelao per trovare \[\frac{\overline{A_{i-1}C_i}}{\overline{C_iB_i}}=\frac{i+1}{n-i}.\]
- Usa la similitudine \(\triangle A_nA_{i-1}B_i \sim \triangle H_iA_{i-1}C_i\) per determinare \[\overline{C_iH_i} = \frac{i(i+1)}{n(n+1)}.\tag{1}\label{eq2813:1}\]
- Osserva che l’equazione \eqref{eq2813:1} è valida anche per il triangolo più a sinistra, la cui altezza è pari a \(1\).
- Concludi che l’area ombreggiata è uguale a \[\mathcal A(n)=\frac1{2n^2(n+1)}\sum_{i=1}^n i(i+1).\]
- Usa i risultati noti \(\sum_{i=1}^n i = \frac{n(n+1)}2\) and \(\sum_{i=1}^n i^2 = \frac{(2n+1)n(n+1)}6\) per calcolare l’espressione, \[\mathcal A(n) = \frac{n+2}{6n},\] cosicché l’area richiesta tende a \(\frac16\) quando \(n\to\infty\).
Introduciamo ora un sistema di assi cartesiani con origine in \(O\equiv A_n\).
Considera la spezzata che si ottiene collegando i punti \(B_n\equiv C_n, C_{n-1},\dots,C_2,C_1,C_0\equiv A_0\). Chiameremo \(f_n(x)\) questa funzione. Il nostro obiettivo è quindi quello di trovare un’espressione analitica per \(f(x)\) definita come
\[f(x) = \lim_{n\to\infty} f_n(x).\tag{2}\label{eq2813:2}\]
- Per \(n=1,2,\dots,n\), chiama \(x_i\) e \(y_i\) le ascisse e ordinate, rispettivamente, del punto medio \(M_i\) del segmento \(C_{i-1}C_i\).
- Usa l’equazione \eqref{eq2813:1} e la simmetria del grafico per calcolare \[x_i = \frac{i^2}{n(n+1)}\] e \[y_i = \frac{(n-i)^2}{n(n+1)}.\]
- Scrivi \(y_i\) in funzione di \(x_i\). Troverai \begin{eqnarray}y_i &=& \left(\frac{n}{\sqrt{n(n+1)}}-\sqrt{x_i}\right)^2.\end{eqnarray} Quando \(n\to\infty\) questa espressione tende a \[f(x) = \left(1-\sqrt x\right)^2.\]
- Verifica che \[\mathcal A_{\infty} = \int_0^1 f(x) dx = \frac16.\]
Vogliamo ora mostrare formalmente la convergenza \eqref{eq2813:2}, e verificare che la convergenza è uniforme. Fissiamo quindi un \(\varepsilon>0\).
- Usando i risultati sin qui ottenuti, mostra che \begin{eqnarray}|f_n(x_i) -f(x_i)|&\leq& \left| \frac{n^2}{n(n+1)}-1+\right.\\&+&\left. 2\left(1-\frac{n}{\sqrt{n(n+1)}}\right) \right|\underset{n\to\infty}{\to} 0.\end{eqnarray}Quindi è possibile scegliere \(N_1\) in modo tale che la quantità appena scritta sia minore di \(\frac{\varepsilon}3\) per ogni \(n> N_1\).
- Dato un punto di coordinate \((x,f_n(x))\), che giaccia, ad esempio, tra \(C_{i-1}\) e \(C_i\), dimostra che \begin{eqnarray}|f_n(x_i)-f_n(x)| &\leq& \overline{C_nC_{n-1}} =\\&=& \frac{2n}{n(n+1)}\underset{n\to\infty}{\to} 0.\end{eqnarray}Puoi pertanto scegliere \(N_2\) in modo che tale distanza sia minore di \(\frac{\varepsilon}3\), per ogni \(n> N_2\).
- \(f(x)\) è uniformemente continua in \([0,1]\) (perché?), il che ci permette di garantire \[|f(x_i) – f(x)| < \frac{\varepsilon}3,\] purché sia \[|x_i-x| < \delta,\tag{3}\label{eq2813:3}\] per un qualche \(\delta>0\) indipendentemente da \(x\). Nota che \[|x_i-x| \leq \overline{C_1A_n} = \frac{2n}{n(n+1)} \underset{n\to\infty}{\to} 0,\]così che \eqref{eq2813:3} è soddisfatta per \(n\) sufficientemente grande, diciamo \(n> N_3\).
- Usando la disuguaglianza triangolare, mostra che \begin{eqnarray}|f_n(x) -f(x)| &\leq& |f_n(x)-f_n(x_i)| + \\&+&|f_n(x_i) – f(x_i)| +\\&+& |f(x_i) – f(x)|< \varepsilon\end{eqnarray} per ogni \(n>\max(N_1,N_2,N_3)\), per ogni \(x\in [0,1]\), e concludi che la successione \((f_n(x))\) converge a \(f(x)\) uniformemente.
