Ci occupiamo del comportamento di successioni ottenute mediante convoluzione. In particolare mostreremo delle condizioni sufficienti sulle successioni di partenza affinché la successione ottenuta convolvendole sia infinitesima.
Date due successioni \(a_n\) e \(x_n\), \(n=0,1,2\dots\), definiamo convoluzione tra di esse una nuova successione ottenuta sommando i prodotti di ciascun termine della prima sequenza con il corrispondente termine di una versione “ribaltata” e “traslata” dell’altra sequenza. In particolare il termine \(n\)-esimo della nuova successione sarà dato da
\[y_n = \sum_{k=0}^n a_{n-k}x_k.\]
Enunciamo e subito dimostriamo il seguente Teorema.
Teorema. Sia \((x_n)\), \(n=0,1,2,\dots\) una succesione infinitesima e \(\sum_{k=0}^{+\infty}a_n\) una serie assolutamente convergente. Allora la successione \((y_n)\) definita da
\[y_n = \sum_{k=0}^n a_{n-k}x_k\]
è infinitesima.
Supponiamo che \(\left(\sum |a_n|\right) \to L\). Fissato \(\varepsilon>0\), scegliamo \(N_1\) in modo che, per \(n>N_1\), si abbia
\[|x_n| < \frac{\varepsilon}{2L}.\]
Ricorda inoltre che, essendo una sequenza convergente, \((x_n)\) è limitata, ovvero esiste una quantità positiva \(M\) tale per cui
\[|x_n|<M\]
per ogni \(n\).
Utilizzando la disuguaglianza triangolare otteniamo
\begin{eqnarray}\left|y_n\right| &=&\left| \sum_{k=0}^n a_{n-k}x_k\right|\leq\\&\leq&\left|\sum_{k=0}^{N_1}a_{n-k}x_k\right| + \left|\sum_{k=N_1+1}^n a_{n-k}x_k\right| \leq \\&\leq&\sum_{k=0}^{N_1}\left|a_{n-k}\right|\cdot \left|x_k\right| + \sum_{k=N_1+1}^n\left| a_{n-k}\right|\cdot\left|x_k\right|<\\&<&M\sum_{k=n-N_1}^{n}\left|a_{k}\right| + \frac{\varepsilon}{2L}\sum_{k=0}^{n-N_1-1}\left| a_{k}\right|\tag{1}\label{eq2859:1}.\end{eqnarray}
La convergenza assoluta di \(a_n\) ci dà
\[\sum_{k=0}^{n-N_1-1}|a_k| < L\]
per ogni \(n\). Dal criterio di Cauchy sulla medesima serie, otteniamo
\[\sum_{k=n-N_1}^n|a_k|<\frac{\varepsilon}{2M},\]
per \(n>N_2\). Dalla \eqref{eq2859:1}, se \(n>N_2\) si ricava
\begin{eqnarray}|y_n| &<& M\frac{\varepsilon}{2M} + \frac{\varepsilon}{2L} L =\\&=& \varepsilon.\end{eqnarray}
\(\blacksquare\)
Come esercizio, ti propongo di dimostrare che la successione definita ricorsivamente da
\[y_{n+1} = \frac{n}{n+1}+\frac23 \cdot y_n,\ \ n=0,1,2\dots,\]
con \(y_0\) arbitrario, converge a \(3\). Qui sotto vedi la rappresentazione grafica dei primi valori della successione ottenuta con valore inziale \(y_0=-3,1,10\), rispettivamente.
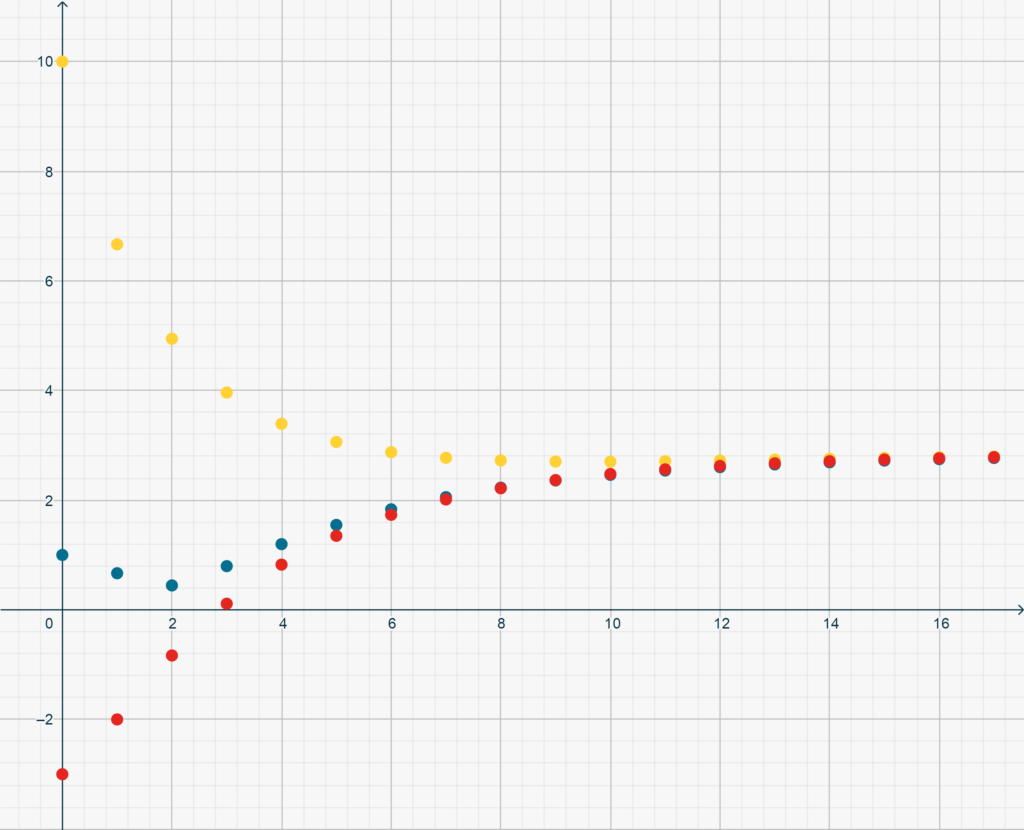
Suggerimento. Riscrivi la ricorsione con il cambio di variabile \(z_n = y_n -3\). Esprimi quindi \(z_n\) come\[z_{n} = \sum_{k=0}^n\left(\frac23\right)^{n-k}x_k,\]con \[x_n =\begin{cases} z_0 & (n=0)\\-\frac1{n+1} & (n>0),\end{cases}\]e usa il Teorema appena dimostrato per ricavare che \((z_n) \to 0\).
