Patire per la tangente

Osserviamo alcune identità che coinvolgono la funzione arcotangente e appaiono piuttosto ‘misteriose’.

$$\begin{equation}\frac{1}{2}\cdot \arctan x + \arctan\left(\sqrt{1+x^2}-x\right)= \frac{\pi}{4}, \ \ \forall x \in \Bbb R,\tag{1}\label{eq229:1}\end{equation}$$

$$\begin{equation}\arctan x = 2\arctan\left(\frac{x}{1+\sqrt{1+x^2}}\right) , \ \ \forall x \in \Bbb R ,\tag{2}\label{eq229:2}\end{equation}$$

$$\begin{equation}\arctan x + \arctan\left(\frac{x+1}{x-1}\right)=\frac{3\pi}{4}, \ \ \mbox{per} \ \ x >1,\tag{3}\label{eq229:3}\end{equation}$$

Si possono rapidamente dimostrare verificando prima di tutto che la derivata del primo e del secondo membro sono uguali, ovvero che le due quantità differiscono al più per un termine costante. Inserendo poi al posto della $x$ un numero arbitrario scopriamo che tale costante, in effetti, è $0$.

Un procedimento dimostrativo più ‘essenziale’ e più illuminante sul significato geometrico di queste relazioni fa uso esclusivamente della definizione trigonometrica di tangente e arcotangente. Quest’ultima infatti, pur di rimanere soltanto all’interno del primo quadrante, esprime semplicemente la misura dell’angolo acuto di un triangolo rettangolo con un dato rapporto tra la lunghezza dei cateti. Le relazioni poi possono essere estese tenendo conto della simmetria dispari di queste funzioni. Vediamo, ad esempio, come dimostrare geometricamente l’identità $\eqref{eq229:1}$.

---

Supponiamo, per il momento, che sia $x\geq 0$. Considera la seguente Figura.

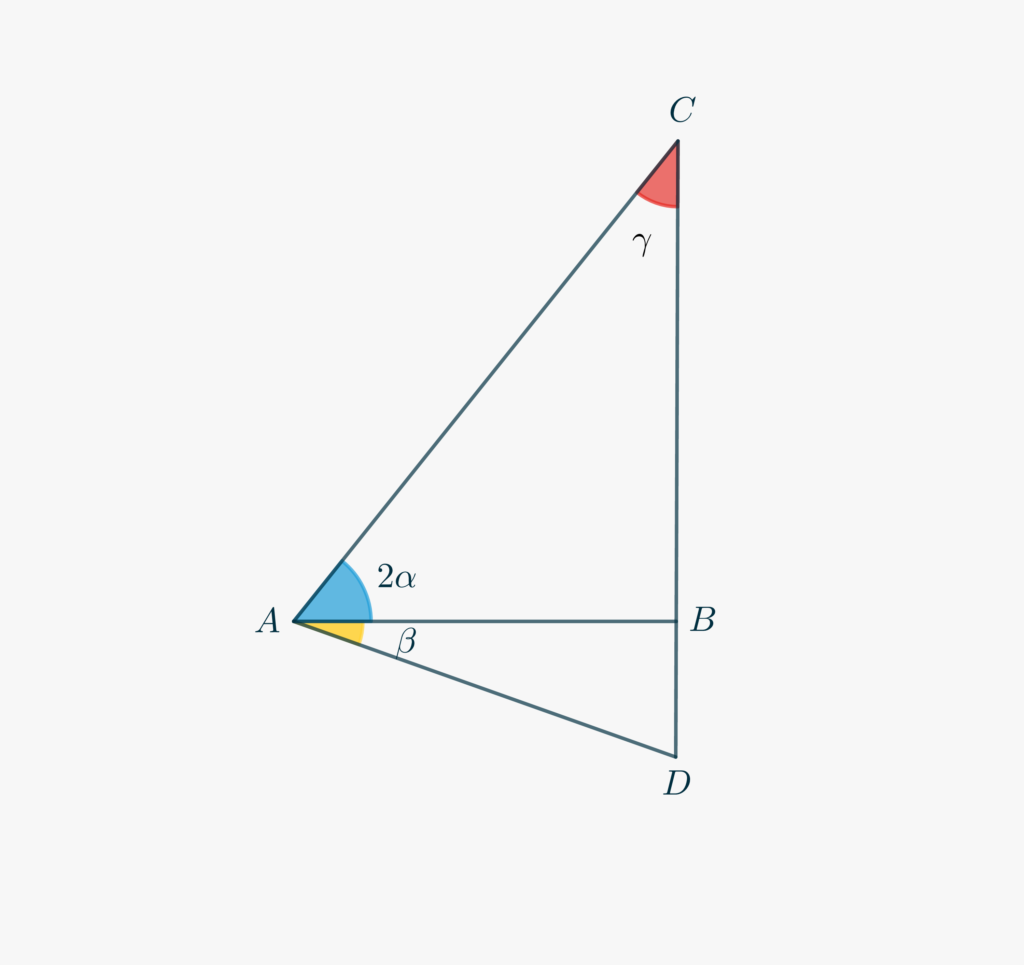
Il triangolo $\triangle ABC$ è rettangolo in $B$ e tale per cui $\overline{AB} = 1$ e $\overline{BC} = x$. Per definizione è

$$\begin{equation}\angle BAC = 2\alpha = \arctan x.\tag{4}\label{eq229:a}\end{equation}$$

Inoltre il Teorema di Pitagora ci dà $\overline{AC} = \sqrt{1+x^2}$. Prolunga ora il segmento $BC$ dalla parte di $B$ fino al punto $D$, in modo che sia $\overline{CD} = \overline{AC}$. Quindi $\overline{BD} = \sqrt{1+x^2}-x$, e, per definizione

$$\begin{equation}\angle BAD = \beta = \arctan\left(\sqrt{1+x^2} -x\right).\tag{5}\label{eq229:b}\end{equation}$$

Dal momento che $\triangle ABC$ è rettangolo, abbiamo

$$\begin{equation}\angle ACB = \gamma = \frac{\pi}{2}-2\alpha.\tag{6}\label{eq229:c1}\end{equation}$$

Il triangolo $\triangle ACD$ è isoscele. Per cui

$$\begin{equation}\gamma = \pi – 2\cdot(2\alpha +\beta).\tag{7}\label{eq229:c2}\end{equation}$$

Uguagliando $\eqref{eq229:c1}$ e $\eqref{eq229:c2}$ si ricava

$$\alpha +\beta = \frac{\pi}{4},$$

ovverosia, usando le definizioni $\eqref{eq229:a}$ e $\eqref{eq229:b}$,

$$\frac{1}{2}\cdot \arctan x + \arctan\left(\sqrt{1+x^2}-x\right) = \frac{\pi}{4}.$$

---

Resta da dimostrare l’identità nel caso in cui sia $x<0$. A tale scopo avremo bisogno di un triangolo rettangolo con un cateto $AB$ di lunghezza $1$ e un cateto $BC$ di lunghezza $-x$.

1. Disegna il triangolo richiesto e definisci $\alpha$ per avere $$2\alpha = \arctan(-x) = -\arctan x,$$ utilizzando la simmetria dispari della tangente.
2. Prolunga $BC$ dalla parte di $C$ fino al punto $D$, in modo che sia $\overline{CD} = \overline{AC}=\sqrt{1+x^2}$.
3. Definisci $\beta$ in modo tale che $$\beta = \arctan\left(\sqrt{1+x^2}-x\right)$$ (ricorda che $x<0$.)
4. Sfrutta il fatto che il triangolo $\triangle ABC$ è retto, per determinare $\gamma = \angle ADC$ in funzione di $\alpha$ e $\beta$.
5. Sfrutta il fatto che il triangolo $\triangle ACD$ è isoscele, per scrivere un’altra relazione che lega $\gamma$ ad $\alpha$ e $\beta$.
6. Utilizza le due eguaglianze trovate in 4. e 5. per scrivere un’unica relazione tra $\alpha$ e $\beta$, che corrisponderà ancora alla $\eqref{eq229:1}$.

---

Per la dimostrazione della $\eqref{eq229:2}$, puoi basarti sulla Figura sottostante, in cui, partendo dal triangolo rettangolo $\triangle ABC$ con $\overline{AB} = 1$ e $\overline{BC} = x$, il lato $AB$ è stato prolungato, dalla parte di $A$ di un segmento $\overline{AD} = \overline{AC}$. Riesci a ricavare la relazione? (Suggerimento: usa il Teorema dell’angolo esterno per esprimere $\angle BDC$ in funzione di $\alpha$.)

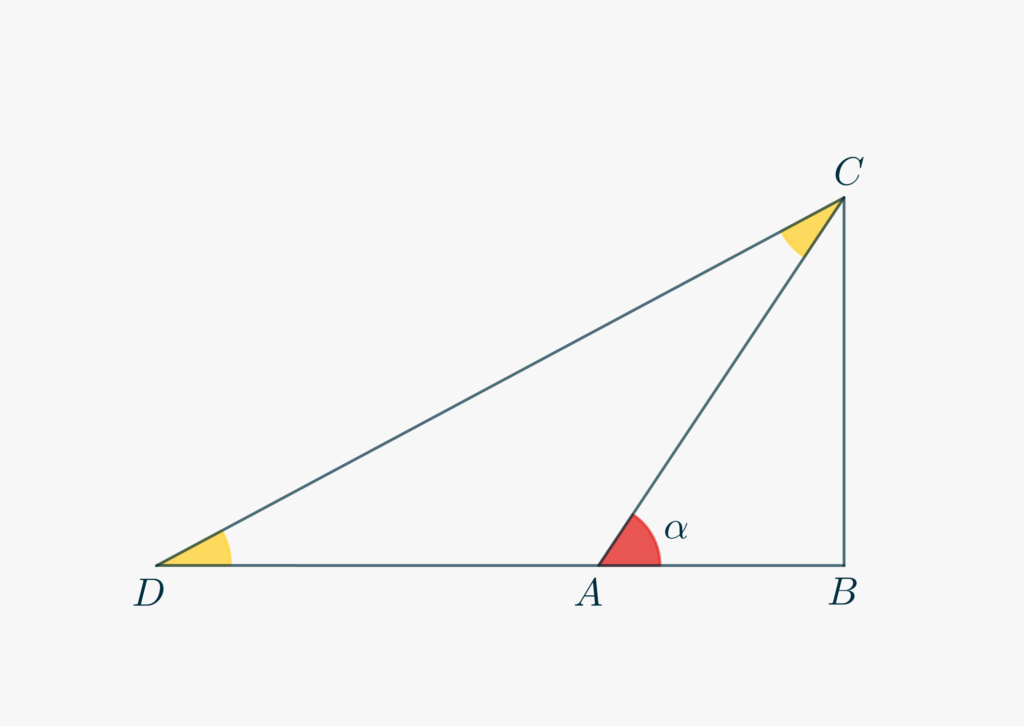
In un prossimo post ti guiderò alla dimostrazione della identità $\eqref{eq229:3}$, e a una sua generalizzazione.